آموزش DSP یا پردازش سیگنال دیجیتال در متلب – قسمت دوم

در جلسه‌ی دوم از این آموزش، به کاوشی عمیق‌تر درباره‌ی پردازش‌ سیگنال دیجیتال می‌پردازیم. با فیلترهای دیجیتال و مشخصات آنها آشنا می‌شویم و یاد می‌گیریم چطور در متلب از آنها برای پردازش سیگنال‌ها استفاده کنیم. در آموزش‌های بعدی نیز موضوع تبدیل فوریه و همینطور مهم‌ترین ویژگی سیگنال‌های صوتی یعنی فرکانس را به طور کامل بررسی خواهیم کرد.

• اگر جلسه اول آموزش را مطالعه نکردین از اینجا مطالعه کنید.

نرم افزار مورد نیاز

• متلب

مرحله ی اول: چگونه سیگنال‌‌ها را در محیط نرم افزار متلب باز کنیم؟

پس از اینکه با استفاده از نرم‌افزار Audacity یک سیگنال صوتی ضبط کردیم (روش آن در جلسه‌ی قبلی همین آموزش توضیح داده شد) حالا می‌خواهیم آن را در نرم‌افزار متلب پردازش کنیم. ابتدا باید بتوانیم آن سیگنال ضبط شده را در محیط متلب بارگذاری کنیم. این کار با استفاده از دستور wavered امکان‌پذیر است که تابعیست که فایل‌های صوتی با پسوند (wav.) را می‌خواند. فایل خروجی از سیگنالی که در Audacity ضبط می‌کنیم نیز با همین فرمت است.

ورودی تابع wavered باید نام سیگنالی باشد که می‌خواهیم آن را پردازش کنیم. در اینجا ما سیگنالی که جلسه قبل ضبط کرده بودیم را داریم که نام آن را testSound.wav گذاشته بودیم و البته زمانی که می‌خواهیم آن را به عنوان ورودی تابع متلب وارد کنیم، تنها کافی است که test Sound را وارد کنیم و وارد کردن پسوند wav. لازم نیست. اما خروجی این تابع چه چیزی خواهد بود؟

• Y: نام سیگنال
• Fs: نرخ نمونه‌برداری از سیگنال
• Bits: تعداد بیت‌ها

اگر به کد زیر دقت کنید، عملکرد این تابع را بهتر متوجه خواهید شد. همچنین این کد به گونه‌ای نوشته شده است که در ضمن پردازش سیگنال، فایل صوتی آن را برای کاربر نیز پخش می‌کند تا کاربر متوجه تغییراتی که در طول زمان اتفاق می‌افتند باشد.

[s0,fs,bits] = wavread(‘testSound’);
sound(s0,fs);
pause(9)
t=(0:length(s0)-1)/fs;
figure
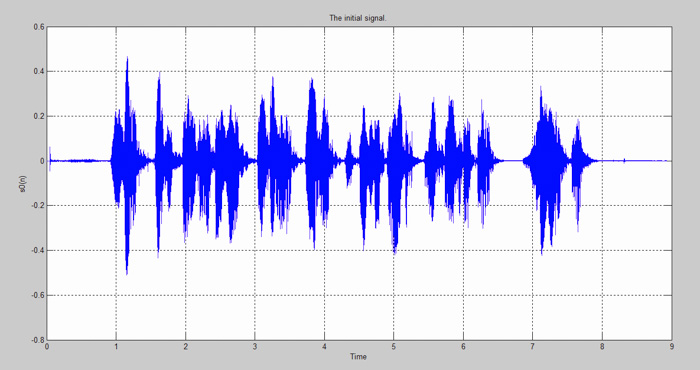
plot(t,s0),grid
title(‘The initial signal.’);
xlabel (‘tTime’)
ylabel(‘s0(n)’);

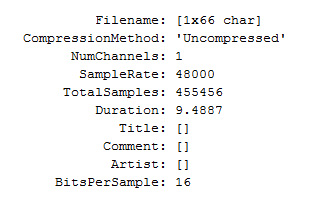
اگر مایل باشید در مورد سیگنال صوتی ضبط شده‌ خودتان اطلاعات بیشتری هم به دست آورید، کافیست که نام فایل صوتی مورد نظر را با پسوند wav. در ورودی تابع audioinfo بنویسید و این تابع به عنوان خروجی ویژگی‌های مختلف آن سیگنال صوتی را به شما اعلام خواهد کرد.

audioinfo(‘testSound.wav’)

از قضا این تابع بسیار تابع کارآمدی محسوب می‌شود. مخصوصا در مواقعی که با یک سیگنال ناشناخته سروکار داشته باشید. مثلا سیگنالی به شما داده شده است که نرخ نمونه‌برداری، گستره‌ی زمانی، bit/sample و چیزهایی از این قبیل که همگی اطلاعات مهمی ‌برای پردازش سیگنال هستند را در مورد آن نمی‌دانید. در این گونه مواقع تابع فوق کار شما را راه خواهد انداخت.

مرحله دوم: حذف مقدار میانگین (مولفه DC) سیگنال

مولفه‌ی DC یا جریان مستقیم، ولتاژ ثابتی است که به شکل موج سیگنال که به صورت خالص متناوب (AC) است، اضافه می‌شود. (هر سیگنالی و در اینجا سیگنال صوتی)

مقدار ولتاژ متوسط واقعی برای یک شکل موج AC خالص همواره صفر است. از طرفی سیگنال صوتی هم آنالوگ است اما زمانی که با نرم‌افزار Audacity به فرم دیجیتال تبدیل می‌شود، یک مولفه DC هم پیدا می‌کند. دلیل این اتفاق هم این است که Audacity سیگنال‌ها را متناسب با بازه‌های قابل قبول خودش مقیاس (scale) می‌کند. معمولا یک سیگنال آنالوگ مقادیری در محدوده‌ی ۰.۵V- تا ۰.۵V دارد.

بنابراین ما باید یک مولفه‌ی DC با مقدار حدودا ۰.۵V داشته باشیم چون Audacity نمونه‌هایی که برمی‌دارد را به سمت مثبت مقیاس می‌کند. (یعنی همه‌ی نمونه‌ها را با یک نسبت ثابت به اعدادی در بازه‌ی ۰ تا N می‌برد که N یک عدد طبیعی است)

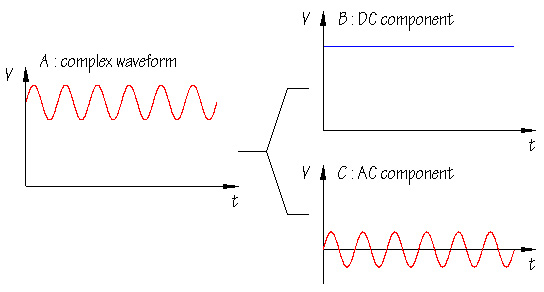
هنگامی‌ که سیگنال شما یک مولفه‌ی DC دارد، مقادیر دامنه‌ی سیگنال در مولفه‌ی AC نیز مقادیری با محوریت این مقدار DC خواهند بود. به عنوان مثال تصویر بالا را ببینید. فرض کنید یک شکل موج سینوسی داریم که دارای دامنه‌ی ۲V p-p (peak to peak) است و می‌خواهیم یک مولفه‌ی دی سی ۰.۵ ولتی به آن اضافه کنیم. سیگنالی که حاصل می‌شود دارای دامنه‌ ولتاژ ۱.۵V در بالاترین نقطه و ۰.۵V- در پایین‌ترین نقطه خواهد بود.

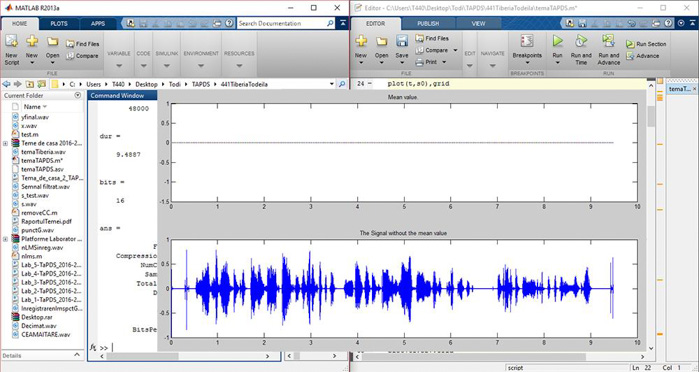
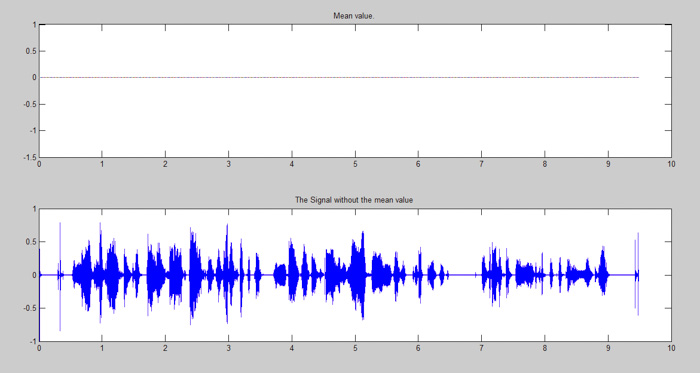
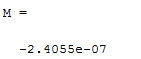
خب، حالا می‌خواهیم عکس این کار را انجام دهیم. یعنی سیگنالی به ما داده شده است و ما اولا می‌خواهیم بدانیم که آیا مولفه DC دارد یا خیر و ثانیا اگر دارد مقدار آن چقدر است. این کار را می‌توانیم با پلات گرفتن از تابع با کد زیر که دستور M یا تعیین میانگین نیز به آن اضافه شده است، انجام دهیم.

M = mean(s0)
figure
subplot(2,1,1), plot(t,M)
title(‘Mean value.’);
s1 = removeDC(s0);
subplot(2,1,2), plot(t,s1)
title(‘The Signal without the mean value’);

قدم مهم بعدی این است که این مقدار DC را در صورت وجود، حذف کنیم. چرا که اصل سیگنال‌های صوتی تولید شده (در حالت آنالوگ) این مولفه را ندارند و ما می‌خواهیم چیزی که پردازش می‌کنیم در نزدیک‌ترین حالت ممکن به سیگنال واقعی باشد. تابع removeDC به همین منظور طراحی شده است. کار کدی که در ادامه می‌بینیم و در آن از این تابع استفاده شده است این است که مقدار میانگین یا همان مولفه DC یک سیگنال را محاسبه کند و آن را از سیگنال کم کند تا دامنه‌ی واقعی سیگنال به دست آید.

function [sOut] = removeDC(sInput)
DC = mean(sInput);
sOut = sInput – DC;
end

مرحله سوم: فرآیند Decimation یا کاهش فرکانس

فرکانس نمونه برداری ما ۴۸/۰۰۰Hz است اما می‌خواهیم آن را به ۱۶/۰۰۰Hz کاهش دهیم. این کار یعنی کاهش نرخ نمونه‌برداری از سیگنال، با فرآیند Decimation و با استفاده از تابعی با همین نام که در متلب وجود دارد، انجام می‌شود.

در حقیقت، زمانی که از یک سیگنال صوتی نمونه‌برداری می‌کنیم، کمترین فرکانس استفاده شده باید ۸KHz باشد و این عدد بر اساس نرخ نایکوئیست به دست می‌آید که دو برابر کمترین فرکانس موجود در طیف شنوایی انسان است.

علت این کاهش سیگنال این است که اولا ببینیم که میان سیگنال اولیه و سیگنال کاهش فرکانس یافته چه تفاوت‌هایی وجود دارد و در ثانی از این تفاوت‌ها برای بهبود سیگنال استفاده کنیم.

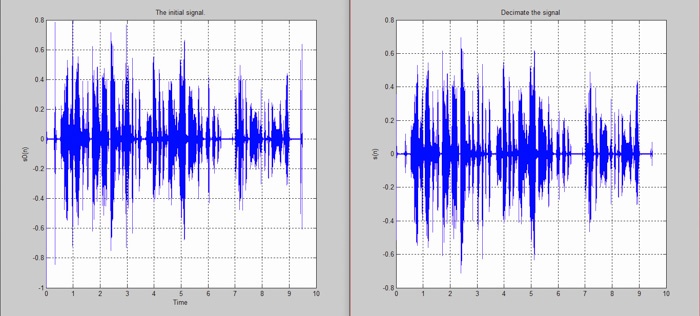
نام دیگر این فرآیند downsampling است. پس از انجام دادن آن شما در واقع یک سیگنال جدید به دست می‌آورید که گویا آن را از سیگنال آنالوگ اصلی اما با  نرخ نمونه‌برداری کمتری گرفته باشید. همانطور که می‌توانید در تصویر زیر ببینید، در سمت چپ تصویر سیگنال آنالوگی قرار دارد که با نرخ نمونه‌برداری بالا از آن نمونه‌برداری شده است. در سمت راست همان سیگنال را می‌بینیم که با نرخ کمتری نمونه‌برداری شده است. این دقیقا مفهوم فرآیند decimation یا downsampling است.

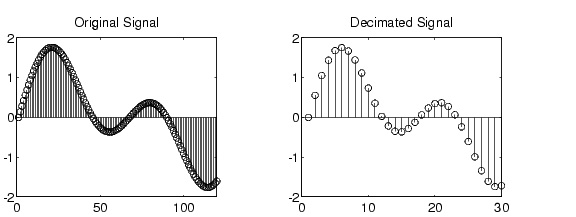
در فرآیندی دیگر، می‌توانیم دقیقا عکس کاری که در بالا انجام دادیم را انجام دهیم که به upsampling گفته می‌شود و حالا دیگر واضح است که در آنجا نرخ نمونه‌برداری را افزایش می‌دهیم تا ببینیم چه نتیجه‌ای رخ می‌دهد. این کار را می‌توانیم با استفاده از روش درون‌یابی (interpolation technique) و یا به کمک یک فیلتر پایین‌گذر انجام دهیم.

fe2=fs/3;
%s2 = decimate(s1,3);
s2 = decimate(s0,3);
t1=linspace(0,length(s2)/fe2, length(s2));
figure
plot(t1,s2),grid
title(‘Decimate the signal’);
ylabel(‘s(n)’);
sound(s2,fe2);
pause(9)

مرحله چهارم: فیلتر کردن سیگنال

یک فیلتر دیجیتال در حقیقت یک تابع کانولوشن زمان گسسته‌ی دامنه گسسته است. اهمیت‌ آنها نسبت به فیلترهای آنالوگ در پردازش سیگنال این است که می‌توانند به صورت همزمان چند عملیات مختلف را انجام دهند. (البته باید این را هم در نظر بگیریم که استفاده از فیلترهای دیجیتال کمی‌ هزینه‌بردارتر است چرا که باید پروسسورهای قوی‌تر و ویژه‌تری برای پردازش سیگنال در اختیار داشته باشیم که بتوانند الگوریتم‌های سنگین و پیچیده‌ی این نوع فیلترها را انجام دهند)

هر فیلتر دیجیتالی، ویژگی‌های خاص و منحصر به فرد خود را دارد؛ مثلا می‌توانند میان‌گذر، میان‌نگذر، فیلتر حذف اعوجاج (ripple) و … باشند. بد نیست قبل از آنکه دوباره به موضوع اصلی بپردازیم، با چند مورد از این ویژگی‌ها و اصطلاحات بیشتر آشنا شویم.

• Passband: بازه‌ی فرکانسی که از یک فیلتر اجازه‌ی عبور پیدا می‌کند.
• فرکانس قطع (Cut-off frequency): فرکانس معینی که توسط کاربر انتخاب می‌شود و به صورت تئوری نشان‌دهنده‌ی مرز فرکانسی قابل عبور است. این عدد باید از نصف فرکانس نمونه‌برداری کمتر باشد تا از aliasing جلوگیری شود. از نظر قوانین الکترونیکی نیز فرکانس قطع جایی است که در آن توان سیگنال نصف می‌شود.
• Stopband: محدوده‌ی فرکانسی که تمام فرکانس‌های بالاتر از آن اجازه‌ی عبور از فیلتر را نخواهند داشت.

فیلترهای دیجیتال را می‌توان به دو گروه تقسیم کرد.

• فیلترهای FIR (finite impulse response – پاسخ ضربه محدود) که می‌توان آنها را با ضرایبی از عددهایی صحیح استفاده کرد.
• فیلترهای IIR (infinite impulse response- پاسخ ضربه نامحدود) که معادل‌های آنالوگ نیز دارند و استفاده از آنها از برخی جهات بهینه‌تر است چرا که فیلترهای با درجات پایین‌تر هم پاسخ مطلوب را می‌دهند.

یکی از ویژگی‌های مهم در این دو نوع فیلتر، مشخصه‌ی فاز آنهاست، FIR دارای مشخصه‌ی فاز خطی و IIR دارای مشخصه فاز غیرخطی (اعوجاج در فاز) است.

ویژگی‌های فیلتر FIR

منظور از داشتن مشخصه‌ی فاز خطی این است که پاسخ فاز در این فیلترها تابعی خطی (دقیقا یک خط مستقیم) از فرکانس است. به همین علت میزان تاخیر این فیلترها در تمام فرکانس‌ها یکسان خواهد بود و در نتیجه منجر به پدیده‌ی اعوجاج فاز یا اصطلاحا phase distortion یا delay distortion نمی‌‌شوند. همین ویژگی در برخی سیستم‌ها مانند مودم‌های دیجیتال، یکی از مهم‌ترین برتری‌های این نوع فیلترها نسبت به فیلتر‌های آنالوگ و IIR محسوب می‌شود.

انواع و اقسام فیلترهای دیجیتال در متلب وجود دارند اما باید بدانیم کدام یک از آنها کاربردی که ما انتظار داریم را برآورده می‌کند. مثلا در این پروژه، علیرغم این مزیت فیلترهای FIR، ما از یک فیلتر IIR استفاده می‌کنیم چرا که به بهره‌وری بالاتری نیاز داریم و با توجه به اینکه فیلترهای IIR در مقایسه با FIR‌ها در درجات پایین‌تری پاسخ مطلوب را به ما می‌دهند، پس یکی از آنها را انتخاب می‌کنیم.

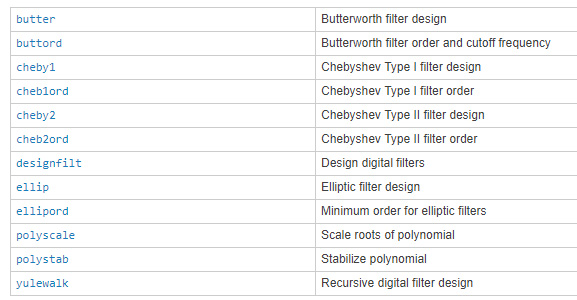
چند خط کد زیر را در متلب بزنید تا یک فیلتر باترورث (Butterworth) به شما بدهد. عملکرد این تابع به این صورت است که شما درجه‌ی فیلتر و فرکانس قطع مورد نظرتان را به آن می‌دهید و به عنوان خروجی ضرایب فیلتر را به شما خواهد داد.

fn = fe2/2;
fc=3400; % cutoff frequency
[Bd,Ad] = butter(40,3400/fn,’low’);

اگر در قسمت help متلب کلمه ی butter را جستجو کنید، صفحه‌ی اطلاعات و راهنمایی در مورد این تابع را برای شما باز خواهد کرد و در آنجا می‌توانید توضیحات لازم را ببینید. مثلا اینکه چرا فرکانس نمونه‌برداری تقسیم بر دو می‌شود. توضیحی که در آنجا می‌بینیم از این قرار است.

فرم کلی تابع به صورت [b,a] = butter(n,Wn) است و به عنوان خروجی ضرایب یک فیلتر دیجیتال پایین‌گذر باترورث را برمی‌گرداند. Wn فرکانس قطع نرمال شده‌ی این فیلتر است و نرمال‌سازی آن به این صورت است که اگر نصف فرکانس قطع را معادل با ۱ در نظر بگیریم، Wn باید به گونه‌ای مقیاس شود که در بازه‌ی 0.0 <Wn<1.0 قرار بگیرد.

ضرایب محاسبه شده برای فیلتر نیز در متغیرهای Bd و Ad ذخیره می‌شوند.

آشنایی با ترمینولوژی فیلترهای دیجیتال

• ضرایب فیلتر: مجموعه‌ای از مقادیر ثابت که مفهوم استفاده از آنها این است که آنها را در نمونه‌هایی که از یک سیگنال برداشته می‌شود و در چارچوب آن فیلتر دیجیتال دارای تاخیر هستند، ضرب می‌کنیم. در حقیقت تمام فرآیند طراحی فیلتر دیجیتال، تعیین ضرایب ثابت مناسبی است که باعث شوند فیلتر پاسخ فرکانسی مطلوب را تولید کند.
  • در مورد فیلترهای FIR، این ضرایب برابر با پاسخ ضربه‌ی فیلتر تعریف شده‌اند.
• مرتبه‌ یا درجه‌ی فیلتر: یکی از مشخصه‌های مهم تمام انواع فیلترها مرتبه‌ی آنهاست (N). این مرتبه با توجه به تعداد عناصری فعالی که فیلتر را تحقق می‌بخشند، تعیین می‌شود. مثلا در فیلترهای IIR، مرتبه‌ی فیلتر دقیقا برابر با تعداد عناصر تاخیرسازی (delayelement) است که در ساختار فیلتر استفاده می‌شوند. قانونی که به طور کلی وجود دارد این است که هرچه مرتبه‌ی یک فیلتر بالاتر باشد، پاسخ فرکانسی آن بهتر خواهد بود.

یک ویژگی مهم دیگر پاسخ فرکانسی است. در حالت ایده‌آل دوست داریم این پاسخ به صورت مستطیلی کامل، با دامنه‌ی ۱ و فرکانس قطع ۰.۵ باشد.  اما در دنیای واقعی می‌تواند حالت‌های غیر ایده‌آل و مختلفی داشته باشد که برای کاربردهای مختلف از آنها استفاده می‌شود.

تصویر زیر پاسخ فرکانسی یک فیلتر دیجیتال را نشان می‌دهد. فیلتری که ما طراحی کردیم؛ در قسمت passband کاملا مسطح است و از طرفی فرکانس قطع آن نیز برابر با ۳۴۰۰Hz است. به این ترتیب شبیه این است که سیگنال ما با یک فیلتر پایین‌گذر فیلتر شود و پس از عبور از فیلتر، هیچ مولفه‌ی فرکانسی بالاتر از این مقدار نباید داشته باشد. اما همانطور که در تصویر می‌بینید، در ادامه‌ی فرکانس قطع با یک stopband مشخص مواجه نیستیم و به همین دلیل ممکن است شاهد باشیم که فرکانس‌هایی بالاتر از این مقدار نیز در سیگنال حضور داشته باشند. اگر مرتبه‌ی فیلتر را افزایش دهیم این مشکل برطرف خواهد شد.

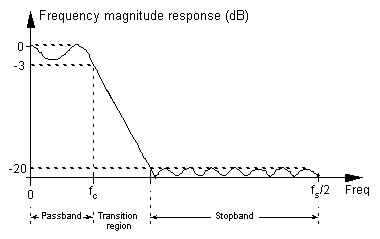
همانطور که در تصویر زیر می‌بینیم، از بین فیلترهای مختلف، فیلتر بیضوی (appreciate) بیش از بقیه به مفهوم فرکانس قطع پایبند است (دقیقا در یک نقطه دارای فرکانس قطع مشخص است) اما با این حال همین فیلتر در قسمت passband دامنه‌ی ثابتی ندارد. هم‌چنین می‌بینیم که فیلترهای چبی شف ۱ و ۲ نیز به ترتیب در قسمت‌های passband و stopband دارای ریپل دامنه هستند. ما از این جهت فیلتر باترورث را انتخاب کردیم که در هیچ کدام از این دو قسمت دارای ریپل دامنه نیست. هرچند که نقطه ضعف آن نیز بزرگ بودن بازه‌ی انتقال بین این دو ناحیه یعنی transition band آن است.

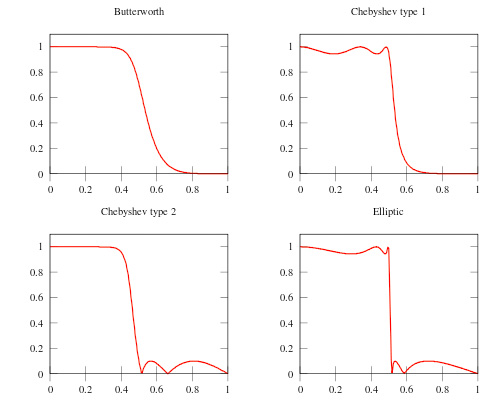
و همانطور که قبلا هم گفتیم مرتبه‌ی فیلتر IIR از مرتبه‌ی فیلتر FIR کوچک‌تر است.

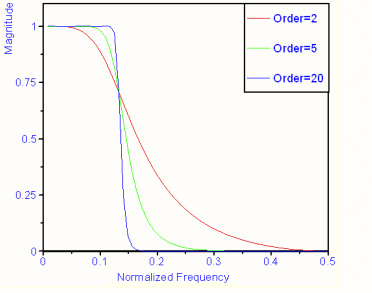
 ما در این پروژه مرتبه‌ی فیلتر را روی ۴۰ تنظیم کردیم به این علت که می‌خواهیم پاسخ فرکانسی تا جایی که امکان دارد به حالت ایده‌آل نزدیک‌تر باشد. در نمودارهای بالا هم می‌توانید این را ببینید که هرچه مرتبه افزایش می‌یابد، پاسخ فرکانسی نیز به فرم ایده‌آل نزدیک‌تر می‌شود.

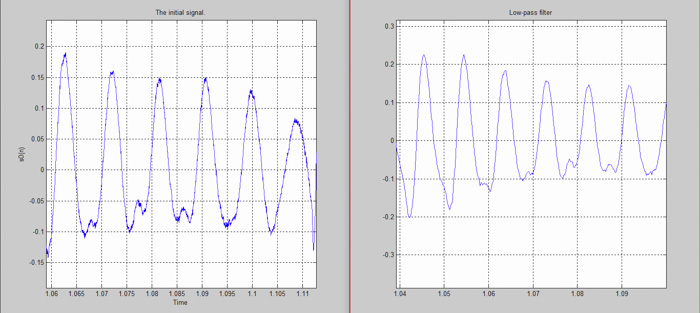
بسیار خب، پس از اینکه سیگنالمان را کاهش فرکانس دادیم (decimate) و از فیلتری که طراحی کردیم نیز آن را عبور دادیم، وقت آن می‌رسد که نتایج را با سیگنال اولیه مقایسه کنیم. این کار را با استفاده از پلات‌های متلب انجام می‌دهیم.

در واقع بهترین روش نتیجه‌گیری در مورد اینکه آیا پردازش‌های ما روی سیگنال پردازش‌های موفق و کارآمدی بوده‌اند یا خیر، مقایسه‌ی نتایج با سیگنال‌های اولیه است. سیگنال اولیه ی ما با نرخ ۴۸KHz نمونه‌برداری شده بود و آخرین سیگنالی که پردازش کردیم دارای نرخ ۱۶KHz است. در تصویر زیر می‌توانیم این دو را با هم مقایسه کنیم و می‌بینیم که سیگنال نهایی نویز کمتری دارد و این نتیجه‌ی خوب و قابل قبولی محسوب می‌شود.

هدف ما در این جلسه آشنایی با ویژگی‌های فیلترهای دیجیتال و تست کردن کارکرد آنها در محیط نرم‌افزار متلب بود. بنابراین تا این لحظه ما در مورد سیگنال‌های صوتی، نرخ نمونه‌برداری و اینکه پردازش‌های مختلف چگونه سیگنال‌های صوتی را تحت تاثیر قرار می‌دهند، مطالبی را یادگرفته‌ایم. در قسمت بعدی، از منظری دیگر به پردازش سیگنال‌های صوتی خواهیم پرداخت و آن چیزی نیست به جز آنالیز فوریه. (تحلیل در حوزه فرکانس)

• منبع: ترجمه از سایت deviceplus.com
• منبع: عکس شاخص از سایت lynda.com

برای آنکه در بهبود کیفیت مطالب ارائه شده به ما کمک کنید، در قسمت کامنت‌ها ما را مطلع کنید که از نظر شما این آموزش چطور بود؟ مهمترین نکته‌ای که از آن آموختید و بهترین ایده‌ای که در ذهن شما ایجاد کرد چه چیزی است؟ پیشنهاد می‌کنم دیگر آموزش های متلب را نیز هم مطالعه کنید.

اگر این نوشته‌ برایتان مفید بود لطفا کامنت بنویسید.